Babai 算法

Babai’s nearest plane algorithm

Babai 算法常用来解决CVP问题，近似因子 $\gamma = 2^{n/2}$

在密码学中，CVP（Closest Vector Problem）是一个基于格的问题，其中要求找到给定格中离目标点最近的点。然而，在实际应用中，我们通常关心的是近似 CVP 问题，也就是找到一个距离目标点不超过最近格点距离的某个因子（通常记作 $\gamma$）的格点

这个因子 $\gamma$ 被称为近似因子。当 $\gamma = 1$ 时，我们就得到了原始的 CVP 问题。当 $\gamma > 1$ 时，我们就允许找到的点与目标点的距离超过最近格点的距离，但不能超过这个距离的 $\gamma$ 倍

近似因子 $\gamma$ 的大小影响了近似 CVP 问题的难度。当 $\gamma$ 越大时，问题就越容易解决，因为允许的解的范围越大。当 $\gamma$ 越小（但大于 1）时，问题就越难解决，因为允许的解的范围越小

（其实CVP问题还有几个不同版本，但就CTF来说，一般是上面那个，其它的看不懂）

举个例子解释一下这个算法

设格 $L \subset R^2$，向量 $v_1 = (137,312),v_2 = (215,-187)$ 是格的基，需要寻找一个 $L$ 中的向量 $v$ ，满足 $||w-v||$ 最小，其中 $w = (53172,81743)$

我们要找的一个最近的向量，即 $w = t_1v_1 + t_2v_2$ ，所以有以下方程

$$
\begin{pmatrix}
53712 & 81743
\end{pmatrix} =
\begin{pmatrix}
t_1 & t_2
\end{pmatrix}
\begin{bmatrix}
137 & 312 \\
215 & -187
\end{bmatrix}
$$

可以解得，$t_1 \approx 296.85,t_2 \approx 58.15$ ,所以接近的向量 $v = 287 (137,312) + 58(215,-187) = (53159,81818)$

计算一下误差 $||v-w|| \approx 76.12$ ，还是比较接近 $w$

但是对于另一组基 $v_1 = (1975,438),v_2 = (7548,1627)$ 也用这种算法，我们得到的 $v’ = (56405,82444)$，计算误差 $||v’-w|| \approx 3308.12$ ，误差较大

对于两组基为什么会得到不太一样的效果呢？这里给大家介绍一下哈达马比例（Hadamard ratio）

$$
H(v_1,v_2) = \left(\frac{\det(L)}{||v_1||||v_2||}\right)^\frac{1}{2}
$$

对于 n 维的情况下，有

$$
H(v_1,v_2,\ldots,v_n) = \left(\frac{\det(L)}{||v_1||||v_2||\ldots||v_n||}\right)^\frac{1}{n}
$$

我们分别计算上面两组基的哈达马比例

对于第一组基

$$
H(v_1,v_2) = \left(\frac{\det(L)}{||v_1||||v_2||}\right)^\frac{1}{2} \approx \left(\frac{92699}{(340.75)(284.95)}\right)^\frac{1}{2} \approx 0.997
$$

非常接近于1

对于第二组基

$$
H(v_1,v_2) = \left(\frac{\det(L)}{||v_1||||v_2||}\right)^\frac{1}{2} \approx \left(\frac{92699}{(2022.99)(7721.36)}\right)^\frac{1}{2} \approx 0.077
$$

非常接近于0

我们把接近于1的基称为好基（Good Basis），接近于0的基称为坏基（Bad Basis）。这里需要提的一点是，哈达马系数的范围是(0,1)的

该题的解题想法，就是Babai算法的思想，找到一个好基，这样我们就可以近似的求出最接近的向量了

具体算法

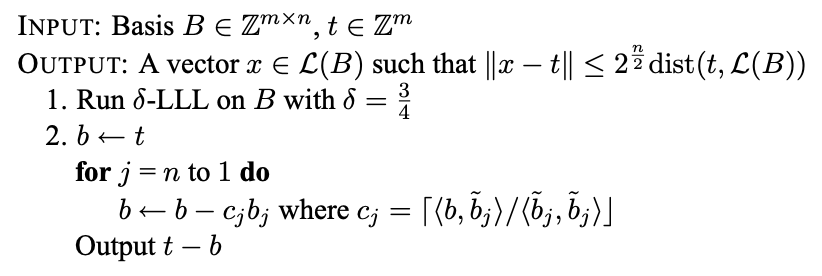
其中 $c_j$ 为 Gram-schmidt 正交化中的系数取整，也即 $proj_{b_j}(b)$ ( $b$ 在$b_j$ 上的投影) 的取整

对于该算法第二步的个人理解(来自于CTF Wiki)：在格基规约和正交化(LLL)过后的基 $B$ 中找到一个最靠近 $t$ 的线性组合

Babai’s Rounding Technique

该算法是Babai’s nearest plane algorithm的一个变种

步骤可以表示为：

N = rank(B), w = target
- B' = LLL(B)
- Find a linear combination [l_0, ... l_N] such that w = sum(l_i * b'_i).
* (b'_i is the i-th vector in the LLL-reduced basis B')
- Round each l_i to it's closest integer l'_i.
- Result v = sum(l'_i * b'_i)

HNP

Hidden number problem

给的质数 $p$ ，许多 $t \in F_p$ 以及每一个的 $MSB_{l,p}(at)$，找出对应的 $a$

• $MSB_{l,p}(x)$ 表示任一满足 $|(x \mod p) - u| \leq \frac{p}{2^{l+1}}$ 的整数 $u$ ，近似为取 $x \mod p$ 的 $l$ 个最高有效位

根据参考三的描述，当 $l \approx \log^{1/2}p$ 时，有如下算法可以解决HNP

我们可以将此问题转化为一个由该矩阵生成的格上的 CVP 问题：

$$
\begin{bmatrix}
p & 0 &\ldots& 0 & 0 \\
0 & p &\ddots& \vdots & \vdots \\
\vdots & \ddots & \ddots & 0 & \vdots \\
0 & 0 & \ldots & p & 0 \\
t_1 & t_2 & \ldots & t_n & \frac{1}{2^{l+1}}
\end{bmatrix}
$$

我们需要在格上找到离 $u = (u_1,u_2,\ldots,u_n,0)$ 最近的向量，所以在这里，我们可以采用 Babai’s nearest plane algorithm 最终我们可以得到一组向量
$v = (a \cdot t_1 \mod p,a \cdot t_2 \mod p,\ldots,\frac{a}{2^{l+1}})$ ，从而算出 $a$

BCTF 2018 - guess_number

服务器端代码

import random, sys
from flag import FLAG
import gmpy2

def msb(k, x, p):
    delta = p >> (k + 1)
    ui = random.randint(x - delta, x + delta)
    return ui

def main():
    p = gmpy2.next_prime(2**160)
    for _ in range(5):
        alpha = random.randint(1, p - 1)
        # print(alpha)
        t = []
        u = []
        k = 10
        for i in range(22):
            t.append(random.randint(1, p - 1))
            u.append(msb(k, alpha * t[i] % p, p))
        print(str(t))
        print(str(u))
        guess = raw_input('Input your guess number: ')
        guess = int(guess)
        if guess != alpha:
            exit(0)

if __name__ == "__main__":
    main()
    print(FLAG)

可以看到，程序一共执行 5 轮，在每一轮，随机的 $α$ 和 22 个随机的 $t_i$，对于每一个 $t_i$，程序会取 $u_i = MSB_{10,p}(a \cdot t_i \mod p)$ ，随后发送给客户端，我们需要根据提供的 $t_i$ 和 $u_i$ 计算出对应的 $a$，可以看到，该问题是一个典型的 HNP 问题，可以使用上述方法解决

import socket
import ast
import telnetlib

#HOST, PORT = 'localhost', 9999
HOST, PORT = '60.205.223.220', 9999

s = socket.socket()
s.connect((HOST, PORT))
f = s.makefile('rw', 0)

def recv_until(f, delim='\n'):
    buf = ''
    while not buf.endswith(delim):
        buf += f.read(1)
    return buf

p = 1461501637330902918203684832716283019655932542983
k = 10

def solve_hnp(t, u):
    # http://www.isg.rhul.ac.uk/~sdg/igor-slides.pdf
    M = Matrix(RationalField(), 23, 23)
    for i in xrange(22):
        M[i, i] = p
        M[22, i] = t[i]

    M[22, 22] = 1 / (2 ** (k + 1))

    def babai(A, w):
        A = A.LLL(delta=0.75)
        G = A.gram_schmidt()[0]
        t = w
        for i in reversed(range(A.nrows())):
            c = ((t * G[i]) / (G[i] * G[i])).round()
            t -= A[i] * c
        return w - t

    closest = babai(M, vector(u + [0]))
    return (closest[-1] * (2 ** (k + 1))) % p

for i in xrange(5):
    t = ast.literal_eval(f.readline().strip())
    u = ast.literal_eval(f.readline().strip())
    alpha = solve_hnp(t, u)
    recv_until(f, 'number: ')
    s.send(str(alpha) + '\n')

t = telnetlib.Telnet()
t.sock = s
t.interact()

LWE

Learning with error

主要关注这样一个式子

$$
A_{m \times n} \cdot x_{n \times 1} + e_{m \times 1} = b_{m \times 1} \mod q
$$

其中 $A$ 是一个 $m \times n$ 的矩阵（公开）（好像m会比n大？如果n比m大的话就是一个长的x映射到一个短的b，就能有多个x映射到b导致不能解密了）； $x$ 是 $n \times 1$ 的向量（明文）； $e$ 是误差，可以看成是每个元素都很小的 $m \times 1$ 的向量（密钥）； $b$ 是 $m \times 1$ 向量（密文）。运算都是在mod q下进行的，q是素数

在知道 $e$ 的情况下，通过上式简单的高斯消元就可以解出密文，即有私钥是容易解的
在不知道私钥 $e$ 的情况下，高斯消元法会放大误差 $e$ ，即只知道公钥和密文是难解的

解法

首先现在问题是

$$
A_{m \times n} \cdot x_{n \times 1} + e_{m \times 1} = b_{m \times 1} \mod q
$$

知道A、b和q，e很小，求x，因为加了e，所以b大概率不会在格A中，但考虑到e很小，如果找到b在格A中最近的向量b`，则有（其实b`是等于b-e ？）：

$$
A \cdot x = b’ \mod q
$$

由于Babai算法不能在模运算之下计算，需要消除 mod q

$$
A \cdot x + kqI_m = b’ - e
$$

$I_m$ 在这里表示一个 $m$ 维的单位矩阵， $k$ 是 $m*1$ 的向量，就是把每一条 $a_ix_i + k_iq = b_i - e_i$ 写成向量和矩阵的形式，就可以构造格（sage有时运行不了就前后交换或者转置）

$$
\begin{bmatrix}
A & qI_m
\end{bmatrix}
\begin{bmatrix}
x \\
k
\end{bmatrix} =
b - e
$$

2020祥云杯 easy matrix

import numpy as np
from secret import *

def random_offset(size):
    x = np.random.normal(0, 4.7873, size)
    return np.rint(x)

secret = np.array(list(flag))

column = len(list(secret))
row = 128
prime = 2129

matrix = np.random.randint(512, size=(row, column))
product = matrix.dot(secret) % prime
offset = random_offset(size=row).astype(np.int64)
result = (product + offset) % prime

np.save("matrix.npy", matrix)
np.save("result.npy", result)

题目就是个LWE的加密，matrix是A、secret是x、offset 是e、result是b、prime是q

按照上面的思路可以写出Sage脚本如下：

#!/usr/bin/env sage
from sage.modules.free_module_integer import IntegerLattice
import numpy as np

def Babai(B, t):
    # not square when using .LLL(), so use IntegerLattice ...
    B = IntegerLattice(B, lll_reduce=True).reduced_basis
    G = B.gram_schmidt()[0]
    b = t
    for i in reversed(range(B.ncols())):
        b -=  B[i] * ((b * G[i]) / (G[i] * G[i])).round()
    return t - b

mx = list(np.load('./matrix.npy'))
rt = list(np.load('./result.npy'))

A = matrix(ZZ, mx)
b = vector(ZZ, rt)
p = 2129
r = A.nrows()
c = A.ncols()

pIr = p*identity_matrix(r)
#M = block_matrix([[A.transpose()], [pIr]])  # [x, k]*[[A.t], [pIr]] = (b-e).t  (but not work ...
M = block_matrix([[pIr], [A.transpose()]])  # [k, x]*[[pIr], [A.t]] = (b-e).t   (this works ...
br = Babai(M, b)

print('e = %s' % (b-br))
R = IntegerModRing(p)
Ar = matrix(R, mx)
secret = Ar.solve_right(br)

m = ''.join(chr(x) for x in secret)
print('m = %s' % m)

---

总结 （2020 Aero CTF Magic ll）

WP
也是 LWE 问题，但是找不到题目源代码，WP里面对于题目只有关键代码的截取，在这里分析一下WP对于Babai算法的实现（加了亿点GPT的注释）

from sage.modules.free_module_integer import IntegerLattice  
from random import randint  
import sys 
from itertools import starmap 
from operator import mul  

# Babai's Nearest Plane algorithm
# from: http://mslc.ctf.su/wp/plaidctf-2016-sexec-crypto-300/
def Babai_closest_vector(M, G, target):  # 定义Babai的最近平面算法
  small = target  # 初始化small为目标向量
  for _ in range(1):  # 进行一次循环
    for i in reversed(range(M.nrows())):  # 从后向前遍历M的每一行
      c = ((small * G[i]) / (G[i] * G[i])).round()  # 计算c，它是small和G[i]的点积除以G[i]的长度的平方，然后四舍五入
      small -= M[i] * c  # 更新small，它是small减去M[i]和c的乘积
  return target - small  # 返回目标向量减去small，这就是最近的向量

m = 100  
n = 12 
q = 1046961993706256953070441  


A_values = [[432963764937, 1734018663110, 341889949567, 1898982667391, 2077151719276, 1407002783602, 1284167537027, 1834426568578, 285492081118, 2058066808411, 682725745551, 212794466530], ...]
b_values = [675829748828112222653599, 19282755083699178123269, 678436649010458903205058, ...]

A = matrix(ZZ, m + n, m)  # 创建一个(m+n) x m的整数矩阵A
for i in range(m):  # 对于每一个i从0到m-1
  A[i, i] = q  # 设置A的对角线元素为q
for x in range(m):  # 对于每一个x从0到m-1
  for y in range(n):  # 对于每一个y从0到n-1
    A[m + y, x] = A_values[x][y]  # 设置A的元素
lattice = IntegerLattice(A, lll_reduce=True)  # 创建一个整数格，并进行LLL减少
print("LLL done")  # 打印"LLL done"表示LLL减少已经完成
gram = lattice.reduced_basis.gram_schmidt()[0]  # 计算格的Gram-Schmidt正交化
target = vector(ZZ, b_values)  # 创建一个目标向量，它是b_values的整数向量
res = Babai_closest_vector(lattice.reduced_basis, gram, target)  # 使用Babai的最近平面算法找到最近的向量
print("Closest Vector: {}".format(res))  # 打印最近的向量

R = IntegerModRing(q)  # 创建一个模q的整数环
M = Matrix(R, A_values)  # 创建一个在模q的整数环上的矩阵，它是A_values
ingredients = M.solve_right(res)  # 解线性方程Mx=res

print("Ingredients: {}".format(ingredients))  # 打印解

for row, b in zip(A_values, b_values):  # 对于A_values和b_values中的每一对元素
  effect = sum(starmap(mul, zip(map(int, ingredients), row))) % q  # 计算乘积的和，然后模q
  assert(abs(b - effect) < 2 ** 37)  # 检查这个值是否接近b

print("ok")  

最前面两个算法脚本里对于Babai的代码实现大体都是相同的（HNP那里因为求解的问题不一样，返回值不一样），在Babai()函数里面实现格基规约和正交化，然后寻找最接近向量，这个脚本和前面的不同点也就是传入Babai()函数前已经完成了格基规约和正交化，具体细节看看GPT给的注释也可以明白

总的来说，Babai算法用来解决维度较小的CVP问题，但是在使用这个算法之前要先使得格基正交化或者准正交化（人话：LLL之后计算格的Gram-Schmidt正交化）

(这里对于 HNP 和 LWE 都只是简单的介绍，后面有时间还会再写，不过题目脚本都是参考的大佬博客，感觉自己上还是不会写，写完博客就刷点题)

参考：
[密码学]格密码学（3）-Babai算法以及GGH公钥密码体制介绍
CTF Wiki
Playing “Hide-and-Seek” in Finite Fields: Hidden Number Problem and Its Applications
用格解LWE——笔记
格密码
Aero CTF 2020 - Magic II (Crypto, 496pts)
Lecture 3 - CVP algorithm