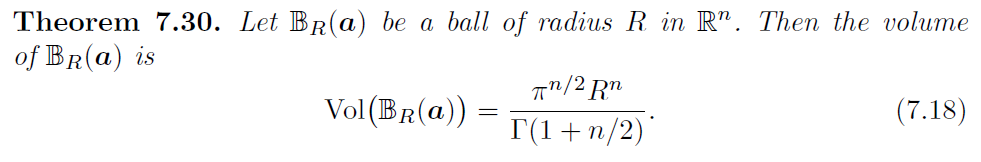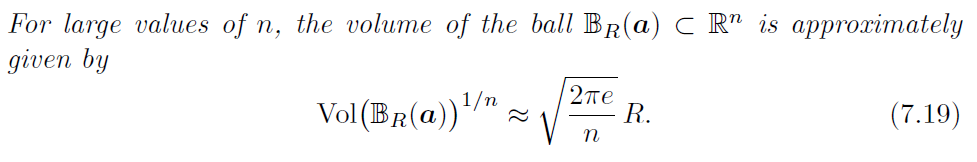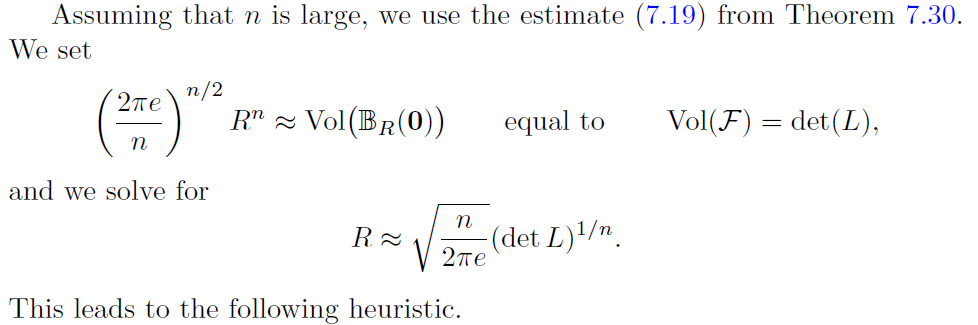格密码学习 LLL算法

Lattice Learning

概念

格是几何空间中按照一定规则排列的无穷点的集合

定义：设 $b_1,b_2,…,b_m$ 是 $m$ 个线性无关的 $n$ 维向量（$n \geq m$），我们取 $c_i \in \mathbb{Z}$，则称以 $c_i$ 为组合系数的 $b_i$ 的线性组合所构成的集合称为 $n$ 维格，即：

$$
A = L(b_1, b_2, \ldots, b_m) = {y | y = \sum c_i b_i, c_i \in \mathbb{Z}}
$$

其中 $B = (b_1, b_2, \ldots, b_m) \in \mathbb{Z}^{n \times m}$ 称为格 $A$ 的一个基，$m$ 称为格 $A$ 的秩，$n$ 称为格 $A$ 的维数。特别的当 $n=m$ 时，称 $A$ 为 $n$ 维满秩格

格 $A$ 的行列式可表示为 $\det(A)$，它是 $n$ 维空间中由格 $A$ 的基向量所生成的平行多面体 $P$ 的体积

对于 $n$ 维满秩格，有 $\det(A) = \sqrt{\det(B^T B)}$ ，我们一般研究的都是满秩格

困难问题

主要有两个类，SVP及CVP

SVP：寻找格L中最短的非零向量，即找到 v^*∈L,对 ∀v∈L ，都有 ||v^*|| <= ||v||

CVP：对于一个非格L的向量Ω,在格中找向量v使得||Ω-v||最小

还有一系列的基于这两个问题的近似问题，其中SVP及CVP问题被证明是NP-hard问题

格攻击理论

（这篇文章主要讲的是LLL算法，主要用来解决SVP问题）

这里的格攻击其实是一个启发式算法，所谓启发式可以大概理解为，你不能证明它是对的，但实际用起来有很好的效果的一些算法

其中用到的最重要的一个东西是高斯启发式

先介绍几个工具再用这个式子

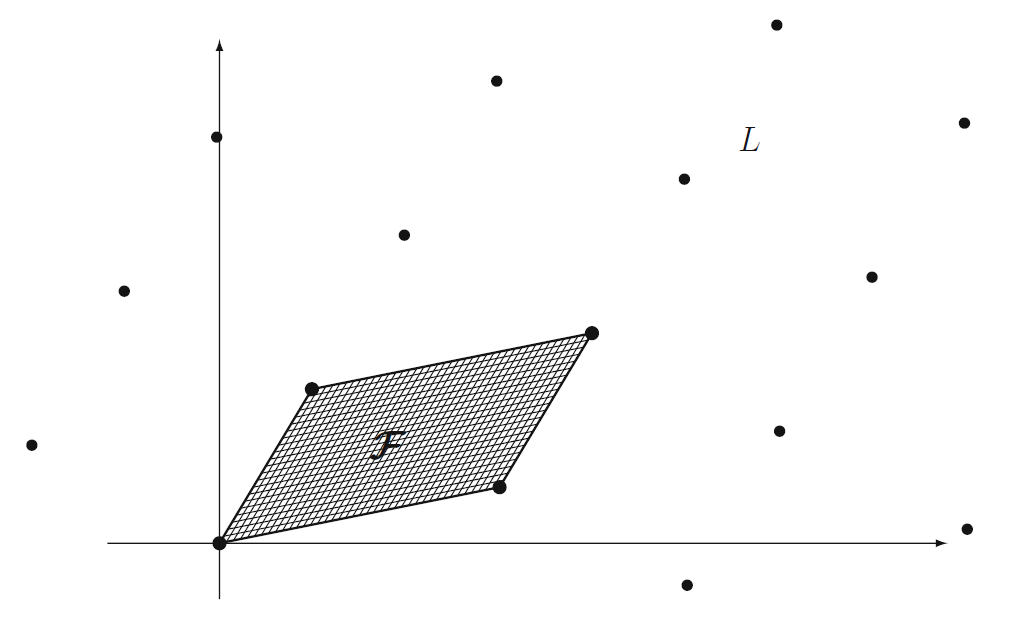
基本域：设 B = [b₁，b₂,…,b_n-1] 为一组格基，则这组格基的基本域为

F(b₁，b₂ ,…, b_n-1) = {t₀b₀ + … + t_n-1b_n-1 (0<=t_i<1)}

从图像上看，F 就是这个格里原点最近的其中“一格”，看图，比如二维中的栗子

后面会用到的是基本域的容积，从结果上看，基本域的容积等于格基的行列式（的绝对值），证明略，可以参考[HPS14]

Vol(F) = det(L(B))

超球体：其实就是高维空间的球体，同样也需要用到它的容积

设 B_R(a) 为一个以点 a 为圆心，半径为 R 的 n 维球体，那么 B_R(a) 的容积（或者说体积）为

这个式子有点复杂，所以一般除了维度较小的情况，不大会用这个式子，而是用它的估算值，在维度 n 足够大时，可以作以下估算

高斯说，一个以零点为圆心的超球体中格点的数量可以用格的基本域的容积估算

把上面式子中向量数量定为1，即可估算只含一个格点的超球半径，即上面高斯启发式的图中的σ(L)
PS：“只含一个格点”其实只是一个估算，实际上因为||v|| = ||-v||，所以随便圈一个球里面应该都有偶数个非零格点

逆向思维一下就是说，长度短于σ(L)的格向量（约）只有一个，所以如果我们通过计算得到一个向量长度（约）小于σ(L)，那么大概率可以确定它是一个最短向量，在维度不高的情况下，可以用LLL把他求出来

最后需要注意的是，这个方法只是一个启发式方法，在实际操作中能不能求到这个最短向量还需要考虑几个东西

格的维度不能太高，不然LLL的准确度不能保证，而且LLL会用很长时间，然后是上面的容积估算也不能保证
格需要“足够随机”，上面图也说了，这只是一个概率估算，所以需要足够随机，后面会说到一些不太随机的格基，比如背包的格和NTRU的格，在实际操作中，这两个问题的格基维度其实都不能太大

格攻击应用

先用一个很简单的问题引入

加密开始，Alice先选择一个大的正整数 q（不一定是素数）为一个公共参数作为公钥，并选择两个秘密的正整数 f,g 作为私钥，其中 f < ^q⁄₂^1/2,^q⁄₄^1/2 < g < ^q⁄₂^1/2 且 gcd(f,q)=1。

然后，Alice可以计算 h ≡ f^-1g (mod q) ，我们可以注意到 f , g 都小于 q^1/2 ,也就是说 f , g 的数量级是O(q^1/2)的级别。而 h 的范围则是O(q)，在 q 很大的时候（比如 q > 2256）时，h 可以说是远大于 f , g 的。这个 h 也将作为公钥。随后，Alice将公钥 q , h 公开。

消息发送方Bob，对信息加密的时候，也需要用到2个参数：明文 m 和一个随机数 r ，其中 m < ^q⁄₄^1/2 , r < ^q⁄₂^1/2 ，然后他就可以计算密文 c ≡ rh + m (mod q)

而收到密文后，Alice的解密过程如下：首先，他计算 a ≡ fc (mod q) 和 b ≡ ad (mod g)，其中 d 是 f 在模 g 意义下的逆元。而神奇的是，对于 a = fc = frh + fm = frf^-1g + fm = rg + fm。然后，我们可以得到 b = ad = drg + dfm ≡ dfm (mod g)。又因为 df ≡ 1 (mod g)，所以我们最后算出来的 b = m 就成立了。

我们从攻击者角度来尝试破解密文

有条件： f，g < ^q⁄₂^1/2，gcd（f，qg）= 1 和 h ≡ f^-1g (mod q)，已知 (q,h)，求 (f,g)

直接使用同余式构造格基好像有点困难，因为LLL规约使用的格基里面的元素都需要在 Z 上，所以不妨先把他展开，展开前先整理一下，因为现在我只知道 f 是小未知数，不能保证 f^-1 也是小未知数，所以先消去逆，两边乘一下 f 即可，得到

fh ≡ g (mod q)

然后可以插入一个未知的 k，把同余式展开，习惯上我会把一个小的未知数放一边（如这里的 g ），方便后续构造格基

hf - qk = g

构造格基的方法其实就是构造出线性方程组，如果你是像我这样把小未知数放等号右边的话，那么一般是等号左边有多少未知数就需要构造多少组方程。现在等号左边有 (f , k) 两个未知数，所以还需要多一个方程，在没有更多的条件可用的情况下，可以插入一些恒等式，比如 f = f ，然后就可以得到

1 · f - 0 · k = f
h · f - q · k = g

把这组线性方程用矩阵-向量的形式表达出来

$$
\begin{pmatrix}
f & -k
\end{pmatrix}
\begin{bmatrix}
1 & h \\
0 & q
\end{bmatrix}=
\begin{pmatrix}
f & g
\end{pmatrix}
$$

把上面的方程对应简写为 vB = w

首先很明显，v 中的 f 和 -k 都是整数，根据格的定义，w 是格基 B 中向量的整数线性组合，所以 w 是以 B 为格基的格 L(B) 中的一个格点

接下来我会期望 w 是 L(B) 的最短向量，这就要用到上面说的估算方法，首先计算一下 w 的长度 ||w|| 和高斯的期望值 σ(L(B))

||w|| = (f² + g²)^1/2 < q^1/2
σ(L(B)) ≈ det(L(B))^1/2 = q^1/2

于是就有 ||w|| <= σ(L(B))，根据前面分析，w 大概率为 L(B) 的最短向量，LLL即可解

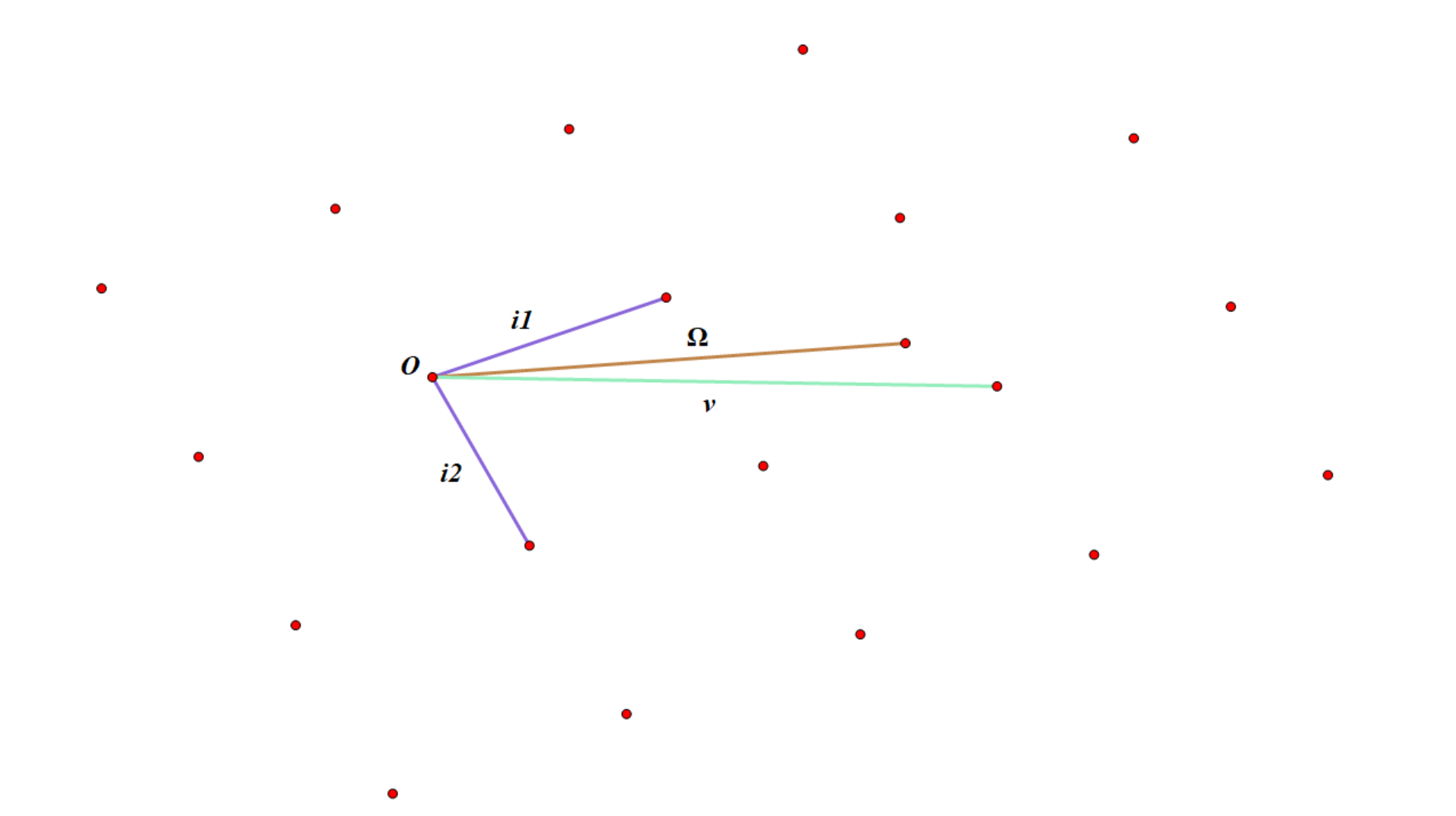
示例

很明显，在这里的一组基是 < i₁ ，i₂ > ，最短向量是 i₂ ，Ω 的最近向量是 v

来道简单的题目试一下

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
bits = m.bit_length()
print(f'{bits = }')

p = getPrime(bits)
q = getPrime(bits)

P = getPrime(bits * 2)
G = (m + p * P) % q
K = (G - m - p * P) // q

print(f'{P = }')
print(f'{G = }')
print(f'{K = }')

# bits = 335
# P = 3394270545570971690577979575406583864946510681585266672410991229280804004453396280771163168409087272659457277569002891388790000326756442550228492597287297623683499025514027403588117117896119108715160651
# G = 60963100282597524831359979973410096860944371822738298396641072874281201661416406035690627807291616264
# K = -1726680592929123430695060700728307617796590011101261305934490117807063551645884305573930787050237014785811531685576831658332832043539071312665804505405023375751155325879443489750916518257143502275697762

分析G,K关系得到 G - m - pP = qK

构造格

$$
\begin{pmatrix}
q & p
\end{pmatrix}
\begin{bmatrix}
K & 0 \\
P & 1
\end{bmatrix}=
\begin{pmatrix}
G-m & p
\end{pmatrix}
$$

如果(G - m, p)刚好是这个格的最短向量，我们就能通过LLL算法在已知K,P下求出(G - m, p)

from sage.all import *
from Crypto.Util.number import long_to_bytes

P = 3394270545570971690577979575406583864946510681585266672410991229280804004453396280771163168409087272659457277569002891388790000326756442550228492597287297623683499025514027403588117117896119108715160651
G = 60963100282597524831359979973410096860944371822738298396641072874281201661416406035690627807291616264
K = -1726680592929123430695060700728307617796590011101261305934490117807063551645884305573930787050237014785811531685576831658332832043539071312665804505405023375751155325879443489750916518257143502275697762

B = Matrix(ZZ,[[K,0],[P,1]])

B = B.LLL()

m = G - B[0][0]

print(long_to_bytes(m))

背包问题

背包问题基于数学的子集和问题，是 Merkle 和 Hellman 在上世纪 70 年代做出的

子集和问题：给定一个正整数集合 M = （m₁，m₂，… ，m_n），及整数S，求出（x₁，x₂，… ，x_n），使得 ∑m_ix_i = S

举个例子：M =（2,3,4,9,14,23），S = （3,4,14），其和等于 21。显然，子集和问题可能有唯一解，可能无解，可能多解。我们只考虑至少有一个解的情况

接下来，我们尝试利用子集和问题的困难性，构建一个公钥密码体系，取

M =（m₁，m₂，… ，m_n）

为公钥，Bob 想发送一条消息，于是将其编码为二进制向量 x =（x₁，x₂，… ，x_n），Bob计算

S = ∑m_ix_i

然后将 S 发送给 Alice，而 Alice 想要解密，必须找到一个合法的 x ，这等价于找到 M 的子集，使之和等于 S

如果 Alice 能快速找到合法的 x 而敌手 Eve 找不到，那么这个密码体系就是有效的，可惜 Alice 并没有这种手段。这个密码体系中没有引入陷门信息，所以 Alice 解密与 Eve 解密的难度是一样的

来考虑如何较快地解决子集和问题（尽管仍然是指数级的），这也是敌手能用上的最好的手段之一。Eve 把 M 划分成两半，然后对于左边那一半，枚举其所有子集 I ，记录子集和 A_I ；对于右边，也同样操作，得到 B_J ，如果存在一对 A_I₀ B_J₀使得它们的和等于 S ，那我们就解决了问题。

之前提到过，Alice 必须有陷门信息，才能快速完成解密，这个公钥密码方案才能有效。接下来我们讨论一种非常简单的子集和问题——超级递增序列上的子集和：

超级递增序列：称一个序列 r = （r₁，r₂，… ，r_n）是超级递增序列，当且仅当满足

∀ 1 <= i <= n-1 ，r_i+1 => 2r_i

也就是说，超级递增序列是指“后一个数比前一个数至少大一倍”的序列。显然就有性质

r_k > ∑^k-1r_i

举个例子：有 $M = (3,11,24,50,115)$ 是超级递增序列，$S = 142$，那么首先检查 $142>155$，故输出 $115$，$S$ 改为 $142-115=27$。接下来 $50$ 被忽略，输出 $24$，$S$ 变为 $3$ 。共输出 $\text{115、24、3}$ ，生成 $x = (1,0,1,0,1)$ ，完成解密。

采用超级递增序列，Alice 是可以快速解密了；但敌手也可以。仍然没有起到添加陷门信息的作用。Merkle 和 Hellman 提出了下面的方案：

Alice 生成一个超级递增序列 $r$，还选择两个保密的整数 $A,B$ 满足

$$
B > 2r_n，gcd(A,B) = 1
$$
Alice 计算一个公钥序列

$$
M \equiv A \cdot r_i \pmod{B}
$$

显然它不是超级递增序列。乘以 $A$ 起到了混淆的作用
Bob 要加密 $x$ ，他发送

$$
S = x \cdot M = \sum_{i=1}^{n} x_iM_i
$$

Alice 要解密 $S$ ，首先计算出

$$
S’ = A^{-1}S \pmod{B}
$$

然后 Alice 求子集和问题 $(r,S’)$ 的解，即可解密
要说明为什么新问题的解就是原问题的解。我们注意到

$$
S’ \equiv A^{-1} \sum_{i=1}^{n} x_iM_i \equiv A^{-1} \sum_{i=1}^{n} x_iAr_i \equiv \sum_{i=1}^{n} x_ir_i \pmod{B}
$$

而 $B$ 是一个非常大的数，故 $S$ 就是 $x \cdot r$ 的确切值

这套公钥加密体系，被称为子集和密码系统，或称背包密码。其核心思想是生成一个超级递增序列，然后用模线性运算进行混淆，将混淆之后的序列作为公钥

接下来，我们看敌手 Eve 如何通过构造格来攻击背包密码。首先，她拿到公钥 $M = (m_1,…,m_n)$ ，然后构造下面的格基

$$
\begin{pmatrix}
x_0,x_1,\ldots,x_{n-1},-1
\end{pmatrix}
\begin{bmatrix}
2 & 0 & 0 & \ldots & 0 & m_1 \\
0 & 2 & 0 & \ldots & 0 & m_2 \\
0 & 0 & 2 & \ldots & 0 & m_3 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & \ldots & 2 & m_n \\
1 & 1 & 1 & \ldots & 1 & S
\end{bmatrix} =
\begin{pmatrix}
2x_0-1,2x_1-1,\ldots,2x_{n-1}-1,0
\end{pmatrix}
$$

现在我们使用LLL算法来尝试攻击背包密码，考虑下面问题：

1
2
3

M = [816358673, 214551389, 683509053, 377954927, 461648693, 819009687, 833612683, 246393449, 258952137, 592274653, 439857687, 164289531, 138621939, 626982035, 733582939, 561376076, 206910526, 470721180, 1105393379, 848577580]
msg = [1,0,1,1,0,1,0,1,1,0,1,0,1,1,0,1,0,1,1,0]
S = 6545130222

构建出格如下：

n = len(M)
L = matrix.zero(n + 1)

for row, x in enumerate(M):
    L[row, row] = 2
    L[row, -1] = x

L[-1, :] = 1
L[-1, -1] = S

运行LLL算法

res = L.LLL()
print(res)

'''
[-1  1 -1 -1  1 -1  1 -1 -1  1 -1  1 -1 -1  1 -1  1 -1 -1  1  0]
[ 2  2  0  2 -2 -2  2 -2  0  0 -4  2  0  0  0  0  0  0  0  0  0]
[ 0  2  0  0  2 -4  0  2  0  0  4 -2  0  0  0  0  0  0  0  0  0]
[-1 -1  1  1  1 -3 -1 -1  1 -1  3 -1 -1  1  3  1 -1  3  1 -1  3]
[ 2  0  0  0  2  2  0 -2  2  0 -4  2  2 -2 -4  2  0  0  0  0  0]
[-1 -1 -1  1  1  1  1 -1 -1  3 -3  1 -1 -1 -1  1 -1  3 -1 -3  2]
[-4  2  0 -2  0  0  2  0  2  2  2 -2 -2  0  0 -2  0  0 -2 -2 -1]
[-1  1  1  1  3 -1 -1 -1  3  1  1 -3 -1  1  1 -3  1 -1  1  1 -1]
[ 1 -3  1  1 -1 -1  1 -1 -3  1 -1 -1 -5  1  1 -1  1  1  1  1  2]
[ 3 -3 -1 -1  1  1 -3 -1 -1  5 -1 -1  1  1 -1  1 -1  1  1 -1  0]
[ 0  2  0  2  4  0 -2  0 -4  0  0  0 -2  0  0 -2  0  0 -2 -2 -1]
[ 2 -2  0  0  2  0 -2  0  0 -2 -4  4  0  0  0  0  0 -2 -2  0 -2]
[ 1  1  1  1 -3 -3  3  1  3  1  1  1 -3 -3  1  1 -1  1  1 -1  0]
[ 1 -1 -1 -1  1 -1 -3 -1 -1  1  1  1  1  3  3 -5  1  1 -1 -1  1]
[-3  1 -3 -1  3  3  3 -1  1 -1  1 -1  1  1 -1  1 -1  1  1 -1  0]
[ 0  0  2  0  0  0  0  2 -2 -2  2 -6  0  0  0 -2  0  0 -2 -2 -1]
[ 0 -2  0 -4  2  0  2  2  0  2 -2  4 -2  0  0  0  0  2  2  0  2]
[-2 -2 -2 -2  2  0 -2 -2  2  0  0  0  2  0  0 -2 -2  0 -2  4  2]
[ 2 -2  0 -2 -4  0  2  0  0  0 -2  0 -2  2  0 -2 -4  0  0 -4  3]
[-2  0  0 -2  0  0  0  0  0 -2 -4  0 -2 -2 -4  2  2  0  0 -2 -1]
[ 1  1 -1  1  1 -1 -1 -1  1 -3 -1 -3 -3 -1  1  1  1  1 -1  1  3]
'''

可以发现第一行的相反向量就是解

拓展维纳攻击

扩展维纳攻击来自《Extending Wiener’s Attack in the Presence of Many Decrypting Exponents》，相关题目在 CTF 中已经出现了，例如 2020 羊城杯的 Simple，但都是一些模板题，在这里记录一下拓展维纳攻击的原理

原理分析

维纳的方法

维纳Wiener提出了一种关于私钥过小时对 $N$ 进行分解的一种方式。并给出了证明当
$$
d < \frac{1}{3}N^\frac{1}{4}
$$
满足时 (还应满足 $q<p<2q$ ，因这里及后文主要是对私钥进行探讨，故忽略这类条件) 一定能够分解$N$

以下为原论文中对于Wiener's Approach的部分描述，部分内容有删减，其实这里也就是维纳攻击的证明，所以要想更详细了解请再看维纳攻击的原理，这里我们主要后面要用到这里的式1，方法如下

已知
$$
e \cdot d - k \cdot \lambda(N) = 1
$$

这里 $\lambda(N) = \text{lcm}(p-1, q-1) = \frac{\varphi(N)}{g} $, 令 $s= 1 - p - q$ ，则有

$$
\begin{align*}
edg - kN = g + ks & (1)
\end{align*}
$$

将两边同时除以 $dgN$ 则有

$$
\frac{e}{N} - \frac{k}{dg} = \frac{g + ks}{dgN} = (\frac{k}{dg})(\frac{s}{N}) + \frac{1}{dN}
$$

我们知道在这里有 $e \approx N$，$s \approx N^{1/2}$，所以有 $\frac{k}{dg} \approx 1$，则我们可以知道等式右边约等于 $N^{-1/2}$，我们都知道当

$$
| x - \frac{a}{b} | < \frac{1}{2b^2}
$$

时则 $\frac{a}{b}$ 是一个连分数近似（连分数定理），即能通过连分数展开覆盖

所以当

$$
d < \frac{\sqrt{2}}{2g}N^{\frac{1}{4}}
$$

时有 $\frac{k}{dg}$ 是 $\frac{e}{N}$ 的连分数近似，即能通过连分数展开覆盖

Guo的方法

郭针对不止一个 $e$ 的情况进行研究，但是郭只研究了两个以及三个 $e$ 的情况

对于两个 $e$ 的情况，我们可以考虑

$$
\begin{align*}
e_1d_1g - k_1(p-1)(q-1) = g \\
e_2d_2g - k_2(p-1)(q-1) = g
\end{align*}
$$

简单化简得到以下式子

$$
\begin{align*}
k_2d_1e_1 − k_1d_2e_2 = k_2−k_1 & (2)
\end{align*}
$$

两边同时除以 $k_2d_1e_2$

$$
\frac{e_1}{e_2} - \frac{k_1d_2}{k_2d_1} = \frac{k_2 - k_1}{k_2d_1e_2}
$$

设 $d_i < N^a$，则等式右边约等于 $N^{-1+a}$
则当

$$
2(k_2d_1)^2 < N^{1+a}
$$

时 $\frac{k_1d_2}{k_2d_1}$ 是 $\frac{e_1}{e_2}$ 的连分数近似，当 $k_2$ 和 $d_1$ 最多为 $N^a$ ，而且 $g$ 很小时，得到

$$
\alpha < \frac{1}{3} - \epsilon （\epsilon > 0）
$$

然而即使我们得到了 $\frac{k_1d_2}{k_2d_1}$ ，还是无法分解 $N$ ，原文后面还讨论了 Guo 的提议，尝试对 $k_1d_2$ 进行分解，这里不再讲解

拓展维纳攻击

为了将分析扩展到 $n$ 个加密指数 $e_i$（解密指数 $d_i$ 很小），我们同时使用维纳和 Guo 的方法，我们将关系

$$
d_ige_i − k_iN = g + k_is
$$

记为维纳等式 $W_i$ ，同样我们可以得到关系

$$
k_id_je_j − k_jd_ie_i = k_i − k_j
$$

记为 Guo 等式 $G_{i,j}$

我们假设 $d_i$ 和 $k_i$ 都小于 $N^{a_n}$ ，且 $g$ 很小，$s \approx N^{1/2}$ ，可以注意到 $W_i$ 和 $G_i$ 的右侧非常小，实际上分别最多为 $N^{1/2+a}$ 和 $N^a$

原文中这里是定义了两个关系式以及指出了他们的大小范围，这个范围很重要也容容易分析处理，之后我们所做的其实就是使用这两个式子的不同复合关系去构造一个格，然后通过求其基向量得到 $\frac{d_1g}{k_1}$，从而可以算得 $\varphi(N)$ 并可以进一步的对 $N$ 进行分解

其实到这里原理分析已经结束，关于格的构造其实也并不复杂，但是核心是这里的复合关系的选取，以及对于最后 $\alpha$ 大小的分析。

两个小解密指数的情况

我们选取关系 $W_1 , G_{1,2} , W_1W_2$，这样便有

$$
d_1ge_1 − k_1N = g + k_1s \\
k_1d_2e_2 − k_2d_1e_1 = k_1 − k_2 \\
d_1d_2g^2e_1e_2 − d_1gk_2e_1N − d_2gk_1e_2N + k_1k_2N^2 = (g+k_1s)(g+k_2s)
$$

我们对第一个关系式乘上 $k_2$，这样左边便全是由 $d_1d_2g^2,d_1gk_2,d_2gk_1$ 和 $k_1k_2$ 构成，这样我们便可以用已知内容构造格将上述式子转化为矩阵运算

$$
\begin{pmatrix}
k_1k_2 & d_1gk_2 & d_2gk_1 & d_1d_2g^2
\end{pmatrix}
\begin{bmatrix}
1 & -N & 0 & N^2 \\
& e_1 & -e_1 & -e_1N \\
& & e_2 & -e_2N \\
& & & e_1e_2
\end{bmatrix}=
\begin{pmatrix}
k_1k_2 & k_2(g+k_1s) & g(k_1−k_2) & (g+k_1s)(g+k_2s)
\end{pmatrix}
$$

等式右边向量的大小为 $N^{2α_2},N^{1/2+2α_2},N^{α_2},N^{1+2α_2}$ , 为了让大小相等，我们可以考虑构造一个 $D$ 矩阵。

$$
D =
\begin{bmatrix}
N & & & \\
& N^{1/2} & & \\
& & N^{1+a_2} & \\
& & & 1
\end{bmatrix}
$$

最终我们构造的矩阵为

$$
L_2 =
\begin{bmatrix}
1 & -N & 0 & N^2 \\
& e_1 & -e_1 & -e_1N \\
& & e_2 & -e_2N \\
& & & e_1e_2
\end{bmatrix} * D
$$

这样向量 $b = \begin{pmatrix}k_1k_2 & d_1gk_2 & d_2gk_1 &d_1d_2g^2\end{pmatrix}$ 便有

$$
|| bL_2 || < 2N^{1 + 2\alpha_2}
$$

这也就是为什么前面需要构造 $D$ 矩阵的原因，给定 $D$ 矩阵后，我们可以得到一个上界，这样问题可以转化为类 SVP 问题

那么这里的 $b$ 向量其实我们使用格基规约算法例如LLL便可以得到基向量 $b$，然后我们求解 $\frac{b_2}{b_1}$ 即得到 $\frac{d_1g}{k_1}$

之后我们就可以得到

$$
\varphi(N) = \frac{edg}{k} - \frac{g}{k} = \left\lfloor \frac{edg}{k} \right\rfloor
$$

我们假设这些格中最短向量长度为 $\Delta^{1/4-\epsilon}$，其中 $\Delta = \det(L_2) = N^{13/2 + a_2}$，如果这些格是随机的，我们甚至几乎可以肯定没有格点比闵可夫斯基界（Minkowski’s bound）大，所以 $bL_2$ 是最短向量当

$$
N^{1+2a_2} < \frac{1}{c_2}(N^{13/2+a_2})^{1/4}
$$

对于一些小的 $c_2$，如果有

$$
a_2 < \frac{5}{14} - \epsilon’
$$

则我们可以通过格基规约找到向量b

三个小解密指数的情况

对于三个指数的情况我们额外选取$G_{1,3} , W_1G_{2,3} , W_2G_{1,3}$

这样我们的向量 $b$ 为

$$
B = \begin{pmatrix}
k_1k_2k_3 & d_1gk_2k_3 & k_1d_2gk_3 & d_1d_2g^2k_3 & k_1k_2d_3g & k_1d_3g & k_2d_3g & d_1d_2d_3g^3
\end{pmatrix}
$$

然后我们便可以构造格

$$
L =
\begin{bmatrix}
1 & -N & 0 & N^2 & 0 & 0 & 0 & -N^3 \\
0 & e_1 & −e_1 & −Ne_1 & −e_1 & 0 & Ne_1 & N^2e_1 \\
0 & 0 & e_2 & −Ne_2 & 0 & Ne_2 & 0 & N^2e_2 \\
0 & 0 & 0 & e_1e_2 & 0 & −e_1e_2 & −e_1e_2 & −Ne_1e_2 \\
0 & 0 & 0 & 0 & e_3 & −Ne_3 & −Ne_3 & N^2e_3 \\
0 & 0 & 0 & 0 & 0 & e_1e_3 & 0 & −Ne_1e_3 \\
0 & 0 & 0 & 0 & 0 & 0 & e_2e_3 & −Ne_2e_3 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & e_1e_2e_3
\end{bmatrix}
$$

其中

$$
D = \text{diag}\left(N^{\frac{3}{2}},N, N^{a + \frac{3}{2}},\sqrt{N}, N^{a + \frac{3}{2}}, N^{a + 1}, N^{a + 1}, 1\right)
$$

同样我们可以得到

$$
|| bL_2 || < 2\sqrt{2}N^{\frac{3}{2} + 2\alpha_3}
$$

则当

$$
a_3 < \frac{2}{5} - \epsilon’
$$

时可以通过格基规约求出向量b

更多解密指数的情况可以看论文或者 CTF Wiki (Xenny大佬编写的)了解

EXP

n = 2 的时候的

e1 = ...
e2 = ...
N = ...
a = 5/14
D = diagonal_matrix(ZZ, [N, int(N^(1/2)), int(N^(1+a)), 1])
M = matrix(ZZ, [[1, -N, 0, N^2], [0, e1, -e1, -e1*N], [0, 0, e2, -e2*N], [0, 0, 0, e1*e2]])*D
L = M.LLL()
t = vector(ZZ, L[0])
x = t * M^(-1)
phi = int(x[1]/x[0]*e1)

n = 3 的时候的

1	`懒得敲，看上面的例子根据2的改就好了`

例题

2020羊城杯 Simple.py

from Crypto.Util.number import *
from Crypto.Cipher import DES
import gmpy2
from secret import flag
import random

key = "abcdefgh"

def des_encrypt(m):
    des = DES.new(key, DES.MODE_ECB)
    res = des.encrypt(m)
    return res

def gen_key():
    p = getPrime(2048)
    q = getPrime(2048)
    n = p * q
    bit = n.bit_length()
    phi_n = (p - 1) * (q - 1)
    num = random.randint(1, 100)
    while True:
        u = getPrime(bit / 4 - num)
        if gmpy2.gcd(u, phi_n) != 1:
            continue
        t = gmpy2.invert(u, phi_n)
        e = bytes_to_long(des_encrypt(long_to_bytes(t)))
        if gmpy2.gcd(e, phi_n) == 1:
            break
    return (n, e)

P = getPrime(1024)
Q = getPrime(1024)
N = P * Q
E = 65537
lcm = gmpy2.lcm(P-1, Q-1)
e1 = gmpy2.invert(getPrime(730), lcm)
e2 = gmpy2.invert(getPrime(730), lcm)
m = bytes_to_long(flag)
c = pow(m, E, N)
print "N = " + str(N)
print "e2 = " + str(e2)
print "c = " + str(c)
_n, _e = gen_key()
_c = pow(e1, _e, _n)
print "_n = " + str(_n)
print "_e = " + str(_e)
print "_c = " + str(_c)

# N = 14922959775784066499316528935316325825140011208871830627653191549546959775167708525042423039865322548420928571524120743831693550123563493981797950912895893476200447083386549353336086899064921878582074346791320104106139965010480614879592357793053342577850761108944086318475849882440272688246818022209356852924215237481460229377544297224983887026669222885987323082324044645883070916243439521809702674295469253723616677245762242494478587807402688474176102093482019417118703747411862420536240611089529331148684440513934609412884941091651594861530606086982174862461739604705354416587503836130151492937714365614194583664241
# e2 = 27188825731727584656624712988703151030126350536157477591935558508817722580343689565924329442151239649607993377452763119541243174650065563589438911911135278704499670302489754540301886312489410648471922645773506837251600244109619850141762795901696503387880058658061490595034281884089265487336373011424883404499124002441860870291233875045675212355287622948427109362925199018383535259913549859747158348931847041907910313465531703810313472674435425886505383646969400166213185676876969805238803587967334447878968225219769481841748776108219650785975942208190380614555719233460250841332020054797811415069533137170950762289
# c = 6472367338832635906896423990323542537663849304314171581554107495210830026660211696089062916158894195561723047864604633460433867838687338370676287160274165915800235253640690510046066541445140501917731026596427080558567366267665887665459901724487706983166070740324307268574128474775026837827907818762764766069631267853742422247229582756256253175941899099898884656334598790711379305490419932664114615010382094572854799421891622789614614720442708271653376485660139560819668239118588069312179293488684403404385715780406937817124588773689921642802703005341324008483201528345805611493251791950304129082313093168732415486813
# _n = 440489238264900860776949063845200558734341182253911040104689726634414488997095518284964514078079911856352824174173937251558842251349762631716798307360995414545464514355957499460396352456341058329671470384493547042182238690727766731554287411757022792467324815342497916894285866240516524768645049867582541899123632009100512965460004548382054578461249990158442675234477122521189649316341623637146867589119951831385717513964941787562068891523060843170463600255518728070958509224053460041184869943038887434435024428311063533345514827827485121055022245800823723487812635502090530820946638405345755666124356919178290008475459419571761406117827422883820901663916276191422633940699113760516149002609672230610575442643822241126824287790055264162725209120192661985259423924307785452001927701323647247782658775780117642900694831475681037634691806232211286493187121464506122012889644137364079403183353774265910554863733455161820449073656744610495110838881353269890437984975607744603113572453211439334880155671730821755361054781243639407912133971530394031933785051770725331242932929244719594830548310768937037042243794551163891451545574837838357398072638709907958216067999891842395376953596940377457308329336524488962532620850237570279134567668379
# _e = 861605654852236668414010386016782729745549477722901970933220380452652052018502113737968204529790495739233258572209422774257139256367928649554562561889013164344608269555777150446651170697255381344437283003508476336814132594917061838422072660017477530465048729471603537912401826065081663165440462979219418291010867656746870617893935758241591032350010782861988742885918015532494020406350897048575155800941991107973433915573030255070411073793489218782862225921465295055907689734413881263179029741870520797816282420230090879687287575328294171448819803530205292587159921154471289747571107461754730577787617451127061265552788125691266357724955508391085485034126227212788895416902189479587194999818764639403752596165043883295506465916277734482380252399557395621566461322664559344483889187037851178431011220134914560438657522787409632677020269086895142488669203469256629173438313487046130238010206678820035631793666627274457756812810094004185303422637897314225624079032617334487815628021058997628511963565055629435278956251869329025544623291223984190562109149316159243565323565271491356378189561005084676592786453581431393651385181326525455441155960432946682976515756161038293313433862078763004704003356983371787414787104076401121444383911561
# _c = 305937839546594439230463861584604201077374759167468410827830943528403007941779658881672477705113617614828611332427199124217887937391378281943856159571057598203709366891547401974326016980711130197275312149966105151573748299654404630150641461765232935912266448303266990247145252052886920248198006212876273661195636104435277145396636985516064154534488750879453474211852461463041960835745695368577903786702607508492658563272121038693371752289017330781719235752018697635304458321008407930986565779826278048082764754367267460637798512780153281325733348999426407049795270044819657399403071013496169060640127279409914638535996355848933378734045908205536540619564723586905257569498716707820544351092379516465943537383422680357333849248129118148543389733395686399565999586899123087310025442994131218237679518267106194962305629529210402269726736072967966518381350920965727690274018080619332676536005722214955949897632990356174168234408837737546230730400434240785496100281815168806724358191550743656843853383646410487436540166360406982096949178466861150173527305369007546917550634679211293496458282787881244581230558011582720632502886494712233308474151958909251857281750741736910202763888790654287328846201724930302778996046434656839999091303411

首先这题分为两部分。第一部分是 gen_key() 以及后面的输出求出 e1，第二部分就是利用 e1,e2 求出 c

第一部分的 t 可以直接DES解密求出来，然后又因为 u 满足 $u<N^{0.25}$ 的条件，所以可以直接用wiener atttack分解出_n，从而求出e1

from Crypto.Util.number import *
from Crypto.Cipher import DES
import gmpy2
from sage.all import *
key = "abcdefgh"
def des_decrypt(m):
    des = DES.new(key.encode(), DES.MODE_ECB)  # Encode the key to bytes
    res = des.decrypt(m)
    return res
def transform(x, y):  # 使用辗转相处将分数 x/y 转为连分数的形式
    res = []
    while y:
        res.append(x // y)
        x, y = y, x % y
    return res


def continued_fraction(sub_res):
    numerator, denominator = 1, 0
    for i in sub_res[::-1]:  # 从sublist的后面往前循环
        denominator, numerator = numerator, i * numerator + denominator
    return denominator, numerator  # 得到渐进分数的分母和分子，并返回


# 求解每个渐进分数
def sub_fraction(x, y):
    res = transform(x, y)
    res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res


def get_pq(a, b, c):  # 由p+q和pq的值通过维达定理来求解p和q
    par = gmpy2.isqrt(b * b - 4 * a * c)  # 由上述可得，开根号一定是整数，因为有解
    x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
    return x1, x2


def wienerAttack(e, n):
    for (d, k) in sub_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        px, qy = get_pq(1, n - phi + 1, n)
        if px * qy == n:
            p, q = abs(int(px)), abs(int(qy))  # 可能会得到两个负数，负负得正未尝不会出现
            return p
    print("该方法不适用")

_n = 440489238264900860776949063845200558734341182253911040104689726634414488997095518284964514078079911856352824174173937251558842251349762631716798307360995414545464514355957499460396352456341058329671470384493547042182238690727766731554287411757022792467324815342497916894285866240516524768645049867582541899123632009100512965460004548382054578461249990158442675234477122521189649316341623637146867589119951831385717513964941787562068891523060843170463600255518728070958509224053460041184869943038887434435024428311063533345514827827485121055022245800823723487812635502090530820946638405345755666124356919178290008475459419571761406117827422883820901663916276191422633940699113760516149002609672230610575442643822241126824287790055264162725209120192661985259423924307785452001927701323647247782658775780117642900694831475681037634691806232211286493187121464506122012889644137364079403183353774265910554863733455161820449073656744610495110838881353269890437984975607744603113572453211439334880155671730821755361054781243639407912133971530394031933785051770725331242932929244719594830548310768937037042243794551163891451545574837838357398072638709907958216067999891842395376953596940377457308329336524488962532620850237570279134567668379
_e = 861605654852236668414010386016782729745549477722901970933220380452652052018502113737968204529790495739233258572209422774257139256367928649554562561889013164344608269555777150446651170697255381344437283003508476336814132594917061838422072660017477530465048729471603537912401826065081663165440462979219418291010867656746870617893935758241591032350010782861988742885918015532494020406350897048575155800941991107973433915573030255070411073793489218782862225921465295055907689734413881263179029741870520797816282420230090879687287575328294171448819803530205292587159921154471289747571107461754730577787617451127061265552788125691266357724955508391085485034126227212788895416902189479587194999818764639403752596165043883295506465916277734482380252399557395621566461322664559344483889187037851178431011220134914560438657522787409632677020269086895142488669203469256629173438313487046130238010206678820035631793666627274457756812810094004185303422637897314225624079032617334487815628021058997628511963565055629435278956251869329025544623291223984190562109149316159243565323565271491356378189561005084676592786453581431393651385181326525455441155960432946682976515756161038293313433862078763004704003356983371787414787104076401121444383911561
_c = 305937839546594439230463861584604201077374759167468410827830943528403007941779658881672477705113617614828611332427199124217887937391378281943856159571057598203709366891547401974326016980711130197275312149966105151573748299654404630150641461765232935912266448303266990247145252052886920248198006212876273661195636104435277145396636985516064154534488750879453474211852461463041960835745695368577903786702607508492658563272121038693371752289017330781719235752018697635304458321008407930986565779826278048082764754367267460637798512780153281325733348999426407049795270044819657399403071013496169060640127279409914638535996355848933378734045908205536540619564723586905257569498716707820544351092379516465943537383422680357333849248129118148543389733395686399565999586899123087310025442994131218237679518267106194962305629529210402269726736072967966518381350920965727690274018080619332676536005722214955949897632990356174168234408837737546230730400434240785496100281815168806724358191550743656843853383646410487436540166360406982096949178466861150173527305369007546917550634679211293496458282787881244581230558011582720632502886494712233308474151958909251857281750741736910202763888790654287328846201724930302778996046434656839999091303411
_t = bytes_to_long((des_decrypt(long_to_bytes(_e))))
_p = wienerAttack(_t,_n)
_q = _n//_p
_d = gmpy2.invert(_e,(_p-1)*(_q-1))
e1 = pow(_c,_d,_n)
print (e1)

e1求出来后就按照拓展维纳攻击来做

from Crypto.Util.number import *
from gmpy2 import invert
c  = 6472367338832635906896423990323542537663849304314171581554107495210830026660211696089062916158894195561723047864604633460433867838687338370676287160274165915800235253640690510046066541445140501917731026596427080558567366267665887665459901724487706983166070740324307268574128474775026837827907818762764766069631267853742422247229582756256253175941899099898884656334598790711379305490419932664114615010382094572854799421891622789614614720442708271653376485660139560819668239118588069312179293488684403404385715780406937817124588773689921642802703005341324008483201528345805611493251791950304129082313093168732415486813
e2 = 27188825731727584656624712988703151030126350536157477591935558508817722580343689565924329442151239649607993377452763119541243174650065563589438911911135278704499670302489754540301886312489410648471922645773506837251600244109619850141762795901696503387880058658061490595034281884089265487336373011424883404499124002441860870291233875045675212355287622948427109362925199018383535259913549859747158348931847041907910313465531703810313472674435425886505383646969400166213185676876969805238803587967334447878968225219769481841748776108219650785975942208190380614555719233460250841332020054797811415069533137170950762289
e1 = 114552459553730357961013268333698879659007919035942930313432809776799669181481660306531243618160127922304264986001501784564575128319884991774542682853466808329973362019677284072646678280051091964555611220961719302320547405880386113519147076299481594997799884384012548506240748042365643212774215730304047871679706035596550898944580314923260982768858133395187777029914150064371998328788068888440803565964567662563652062845388379897799506439389461619422933318625765603423604615137217375612091221578339493263160670355032898186792479034771118678394464854413824347305505135625135428816394053078365603937337271798774138959
N  = 14922959775784066499316528935316325825140011208871830627653191549546959775167708525042423039865322548420928571524120743831693550123563493981797950912895893476200447083386549353336086899064921878582074346791320104106139965010480614879592357793053342577850761108944086318475849882440272688246818022209356852924215237481460229377544297224983887026669222885987323082324044645883070916243439521809702674295469253723616677245762242494478587807402688474176102093482019417118703747411862420536240611089529331148684440513934609412884941091651594861530606086982174862461739604705354416587503836130151492937714365614194583664241
a  = 0.356#731./2049
M1=N**0.5
M2=N**(a+1)
D = diagonal_matrix(ZZ,[N,M1,M2,1])
M=matrix(ZZ,[[1,-N,0,N**2],[0,e1,-e1,-e1*N],[0,0,e2,-e2*N],[0,0,0,e1*e2]])*D
L=M.LLL()
t=vector(ZZ,L[0])
x=t*M**(-1)
phi = int(x[1]/x[0]*e1)
d = invert(0x10001,phi)
m=pow(c,d,N)
print long_to_bytes(m)

参考：
[HPS14] Hoffstein J, Pipher J, Silverman J H, et al. An Introduction to Cryptography[M]. Springer New York, 2014.
Lattice Learning1
格攻击之小未知数方程求解入门——原理与例子
LatticeNotes1
格密码笔记（二）
CTF Wiki
《Extending Wiener’s Attack in the Presence of Many Decrypting Exponents》
密码学硬核笔记——扩展维纳攻击

格密码

#格密码

格密码学习 LLL算法

http://example.com/2024/03/26/格密码学习-LLL算法/

作者

John Doe

发布于

2024年3月26日

更新于

2024年3月30日

许可协议

Babai算法上一篇

AES Padding Oracle Attack 下一篇